深圳实验学校2025年七年级数学下册期末联考试卷免费下载（附答案）

(3分)古希腊哲学家毕达哥拉斯曾说:'美的线型和其他一切美的形体，都必须有对称形式。'下面的图形中，是轴对称图形的是( )

(3分)下列各组数分别是三条线段的长度，其中能围成直角三角形的是()

A. 1, 1, 2

B. 1, 2, 3

C. 3, 4, 5

D. 2, 3, 4

(3分)如图，是一个缺角的△ABC残片，量得∠A=53°,∠B=62°，则此三角形残缺的部分为()

(3分)下列成语所描述事件是必然事件的是()

A.水涨船高

B.守株待兔

C.水中捞月

D.一箭双雕

(3分)下列算式能用平方差公式计算的是()

A. (a+b)(-a-b)

B. (a-b)(-b+a)

C. (2a+b)(a-2b)

D. (a+b+3)(a+b-3)

(3分)如图1，已知AD=AE，添加下列条件仍无法证明△ABE≌△ACD的是()

A. BE=CD

B. AB=AC

C. ∠ADC=∠AEB

D. ∠B=∠C

(3分)如图2，三角板ABC(其中∠A=30°,∠C=90°)和三角板DEF(其中∠E=45°,∠EDF=90°)按照如图所示的位置摆放，点D在边AC上，若AB//EF，则∠FDC的度数为()

A. 8°

B. 10°

C. 12°

D. 15°

(3分)如图3，Rt△ABC与Rt△BCD有公共斜边BC(顶点A、D在BC同侧)，∠BAC=∠BDC=90°，连接AD，已知∠ABD=∠BCA，BD=8，CD=6，则△ABD的面积为()

A. 32

B. 16

C. 12

D. 8

(3分)计算: a⁶÷a³=______

(3分)中国古代数学有着辉煌的成就，《周髀髀算经》《九章算术》《孙子算经》《海岛算经》是我国古代数学的重要文献。某中学拟从这4部数学名著中选择1部作为校本课程'数学文化'的学习内容，恰好选中《孙子算经》的概率是______

(3分)国家卫健委发布《中国青少年健康教育核心信息及释义(2018)版》称，青少年应控制电子产品使用，非学习目的的单次使用时间不宜超过15分钟，每天累计不宜超过1小时，我市调研了部分青少年电子产品使用时间，调研结果整理如下表:

调研总人数50010001500200025003000

使用时长超过1小时的人数3807591137152219002280

使用时长超出规定时长人数的频率0.7600.7590.7580.7610.7600.760

从这3000名学生中任意选取一名学生，其每天使用电子产品时长超过1小时的概率为______

(3分)小亮在一个科学实验课上学习了发声物体的振动实验后，对其作了进一步的探究:在一个支架的横杆点O处用一根细绳悬挂一个小球A，小球A可以自由摆动，如图，OA表示小球静止时的位置。当小明用发声物体靠进小球时，小球从OA摆到OB位置，此时过点B作BD⊥OA于点D，当小球摆到OC位置时，OB与OC恰好垂直(图中的O、A、B、C、D均在同一平面上)，过点C作CE⊥OA于点E。现已知OA=OB=OC=65 cm，测得BD=25 cm，则DE的长为______cm。

(3分)如图，在Rt△ABC中，∠ABC=90°，过B作BM⊥AC于点M，点N为AC边上一点，点P为BC边中点，连接BN，PN，若∠MBA=∠MBN，∠CNP=45°，则MN/CN=______

(8分)计算:

(1) (1/2)⁻² + (-1)²⁰²⁵ + (3.14-π)⁰ + |-2|

(2) a·a⁵ + 2a⁸÷a² - (2a²)³

(6分)先化简，再求值: [(xy+2)(xy-2)-2x²y²+4]÷xy，其中x=10，y=-1/25。

(8分)已知，如图，AD，CE相交于点G，且AD⊥CE。

(1)尺规作图:作线段AD的垂直平分线，垂足为点H，交AE的延长线于点B，交CD于点F;(保留作图痕迹，不写做法，作图请用黑色字迹的笔描黑)

(2)若∠C=∠ABF，求证:△ABH≌△DFH

(8分)小深同学趁假期与朋友去登山。早上8:00，他们从山脚出发，经过40分钟到达山腰休息平台，休息了10分钟后继续前行登上山顶，在山顶停留了半小时后原路下山。如图是他们出发后的时长x(分钟)与他们离山脚的相对高度y(米)之间的关系示意图。请根据图示信息，解答以下问题:

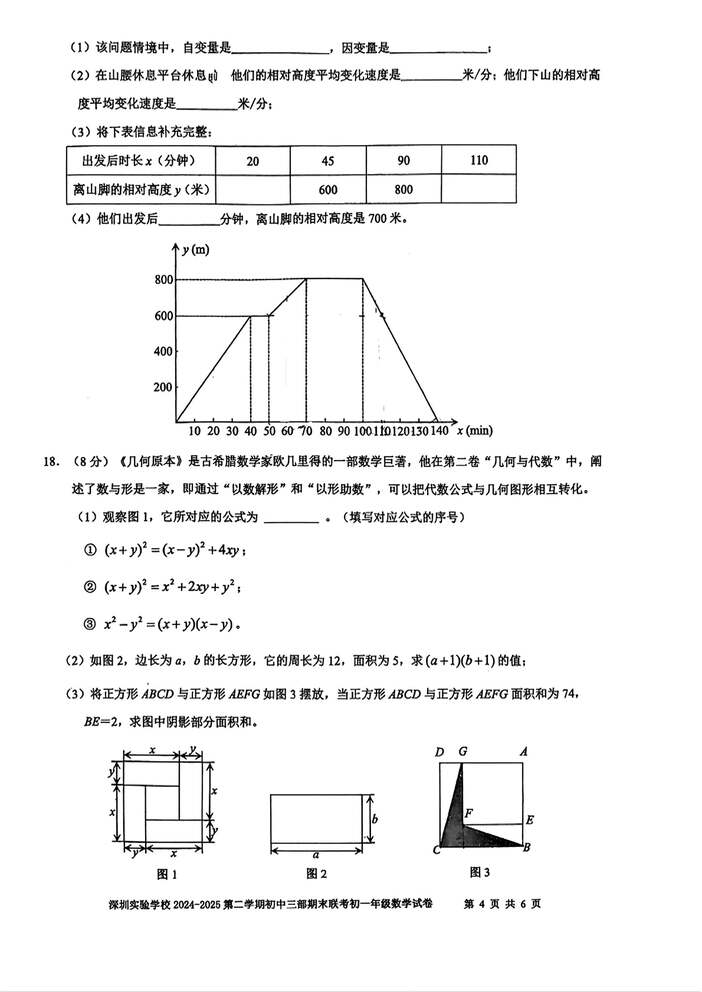
(1)该问题情境中，自变量是______，因变量是______

(2)在山腰休息平台休息(1)他们的相对高度平均变化速度是______米/分;他们下山的相对高度平均变化速度是______米/分;

(3)将下表信息补充完整:

出发后时长x(分钟)204590110

离山脚的相对高度y(米)600800

(4)他们出发后______分钟，离山脚的相对高度是700米。

(8分)《几何原本》是古希腊数学家欧几里得的一部数学巨著，他在第二卷'几何与代数'中，阐述了数与形是一家，即通过'以数解形'和'以形助数'，可以把代数公式与几何图形相互转化。

(1)观察图1，它所对应的公式为______。(填写对应公式的序号)

①(x+y)²=(x-y)²+4xy;

②(x+y)²=x²+2xy+y²;

③x²-y²=(x+y)(x-y)。

(2)如图2，边长为a，b的长方形，它的周长为12，面积为5，求(a+1)(b+1)的值;

(3)将正方形ABCD与正方形AEFG如图3摆放，当正方形ABCD与正方形AEFG面积和为74，BE=2，求图中阴影部分面积和。

(11分)综合实践:数学课上，王老师以'两条线段和的最小值'为题，把'两点之间，线段最短'以及'垂线段最短'两个知识融合在一起展开一节探究活动课。

示例1:将最短路径问题(有人称'将军饮马'问题)转化为数学问题。如图1①，用直线l表示河岸，将军从山脚下的点A出发，到达河岸点C饮马后回到点B宿营，怎样走使他每天所走路程的和最短?

作法是:如图1②，作点B关于直线l的对称点B′，连接AB’与直线l交于点C，则点C即为饮马的地方，此时将军从点A走到点C，再回到点B所走的总路程最短。

示例2，如图1③，要在河岸l上建一座水泵房Q，修建引水渠PQ，使得Q到村庄P的距离最短。施工人员的做法是:过点P作PQ⊥l于点Q，将水泵房建在Q处，这样修建引水渠PQ最短，即省人力又省物力。示例1中所蕴含的数学原理是()

A.两点之间，线段最短

B.垂线段最短

活动二感悟方法，尝试应用

如图2，在等边三角形ABC中，AD是△ABC的中线。

①直接写出BD与AB的数量关系

②若AD=4，点E为AB边的中点，点F为AD上一点，当BF+EF的值最小时，在图2上标注点F的位置，并求出BF+EF的最小值;

活动三迁移拓展，综合应用

如图3，在Rt△ABC中，∠B=30°，点D在斜边BC上，且BC=4CD=4，AE是△BAC的角平分线，点F，点G分别为AC，AE上一点，求DG+FG的最小值。

(12分)几何探究:

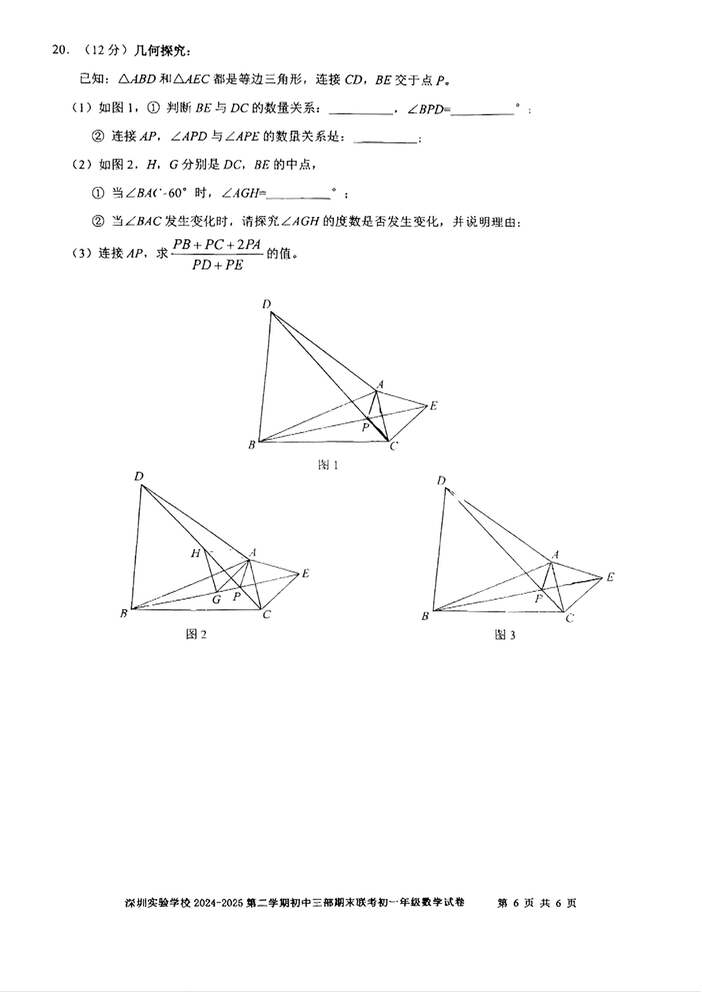
已知:△ABD和△AEC都是等边三角形，连接CD，BE交于点P。

(1)如图1，

①判断BE与DC的数量关系:，∠BPD=

②连接AP，∠APD与∠APE的数量关系是:______

(2)如图2，H，G分别是DC，BE的中点，

①当∠BAC=60°时，∠AGH=______。

②当∠BAC发生变化时，请探究∠AGH的度数是否发生变化，并说明理由:

(3)连接AP，求(PB+PC+2PA)/(PD+PE)的值。