一、选择题
1.由一些大小相同的小正方体组成的几何体从左面和上面看到的图形如图所示,则组成这个几何体的小正方体最少有( )个。
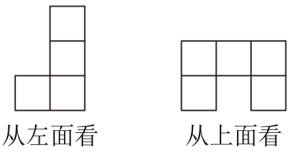
A.6 B.7 C.8 D.9
2.已知x∶y=4∶5,那么x比y( )。
A.多20% B.少20% C.多25% D.少25%
3.下面几种情况中,适合用复式折线统计图描述数据的是( )。
A.某品牌电动车2020-2024年销售情况
B.小力家各项支出占总支出百分比情况
C.六年级各班人数情况
D.北京和上海全年各月平均气温变化情况
4.张老师需要买50本笔记本,三家商店的单价都是9元,甲商店打“八五折”销售,乙商店“买四送一”,丙商店“每满100元减20元现金”。张老师在( )商店买最划算。
A.甲 B.乙 C.丙 D.任一家
5.如图,小圆周长是大圆周长的( ),小圆面积是大圆面积的( )。
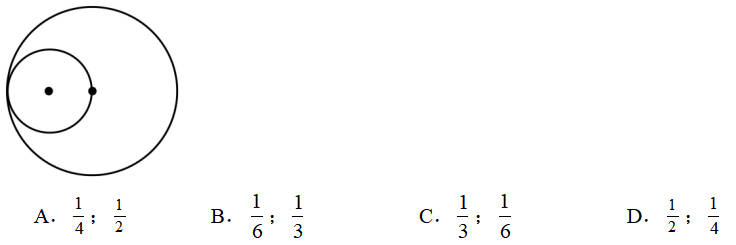
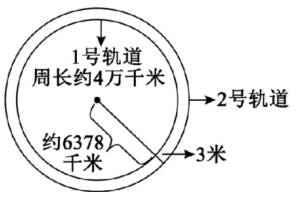
6.科幻片中,要在地球赤道附近修建两条轨道(如图所示)。1号轨道贴近赤道地面,整体呈圆形,2号轨道始终与1号轨道保持3米距离,且2号轨道、1号轨道与赤道所在地球截面在同一平面。为此同学们展开了“2号轨道比1号轨道长多少米”的讨论。你认为说得对的是( )。
淘气说:“只长了不到20米。”
笑笑说:“可能要长几百米。”
奇思说:“可能要长几千米。”
妙想说:“你们说得都不对!赤道那么长,可能要长1万米以上。”
A.淘气 B.笑笑 C.奇思 D.妙想
二、填空题
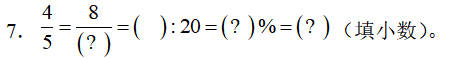
8.文具店一套彩笔定价36元,售出后可获利50%,如果按定价的八折出售,可获利( )元。
9.贴窗花是中国春节的传统习俗,人们以此寄托辞旧迎新、接福纳祥的愿望。下图为一窗花图片,圆的面积是200.96平方厘米,用来裁剪该窗花的最小正方形的周长是( )厘米,面积是( )平方厘米。

10.如图是王叔叔复制一份文件的信息。(M是文件大小的单位)
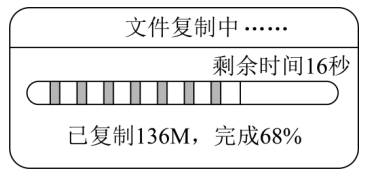
(1)图中68%表示的意义是( );
(2)这份文件一共有( )M。
11.填一填。
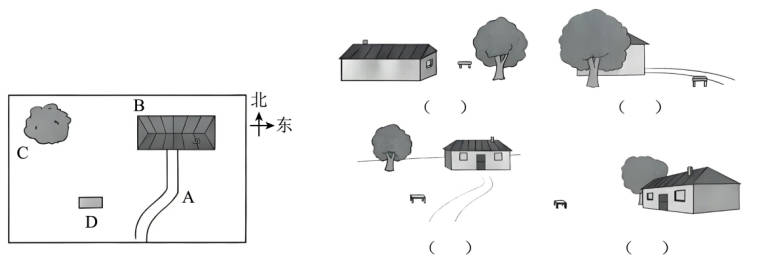
下面左面的图是从空中看到的情况,右面四幅图分别是A、B、C、D哪个位置看到的?填一填。
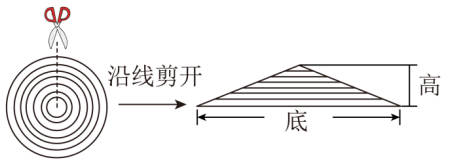
12.把一个半径为3cm的草编圆形茶杯垫按下图的方法剪开,得到的三角形底是( )cm,高是( )cm,面积是( )。
三、判断题
13.圆的周长总是它的直径的3.14倍。( )
14.甲、乙分一堆苹果,甲分到的苹果比乙多,那么甲、乙分到的苹果个数比为。( )
15.一场乒乓球比赛,有10名学生参加。如果采用单循环赛(每两名同学都要赛一场),一共需要赛20场。( )
16.一种商品先涨价15%,再降价15%。它的价格没有发生改变。( )
17.要表示小林在一天中进行各种活动所用的时间是多少,用扇形统计图最合适。( )
四、计算题
18.直接写出得数。
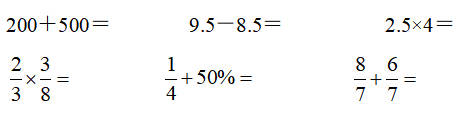
19.脱式计算,能简算的要简算。
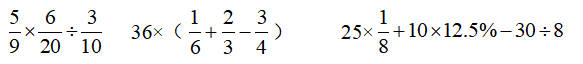
20.解方程。
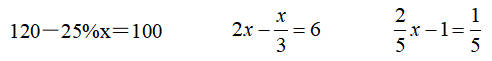
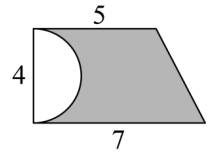
21.求下边图形中阴影部分的面积。(单位:厘米)(π取3.14)
五、作图题
22.在方格纸上分别画出从不同方向观察左边立体图形所看到的形状。

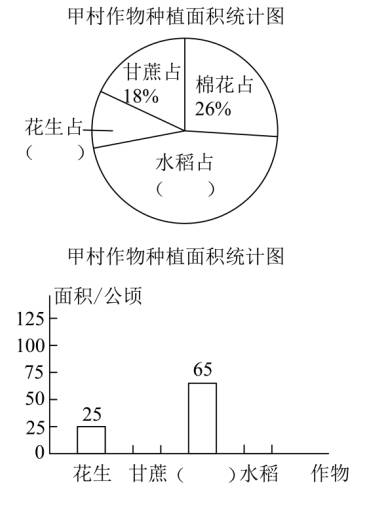
23.甲村有耕地250公顷,根据下面的数据,将两幅统计图补充完整。
六、解答题
24.某车间原计划制造一种零件,每个零件需用钢材3/4千克,改进技术后,每个零件所用的钢材比原来节约1/6。照这样计算,现在做400个这样的零件需要钢材多少千克?
25.一个直角三角形的三条边的长度比是3∶4∶5,周长是60厘米,它的面积是多少平方厘米?
26.学校手工小组要做一个剪纸作品,需要准备一张长条彩纸。李老师去仓库查看材料,发现以下信息:A卷彩纸总长24米,已经用掉了5/8;B卷彩纸总长20米,还剩35%没用。剪纸作品需要一张8米长的完整彩纸。李老师应该选择哪卷彩纸比较合适?
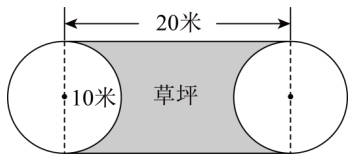
27.某广场的形状与大小如图,两边是两个圆形喷水池,场地中间是绿色草坪,广场的周长是多少?草坪的面积是多少?
28.在淡季客源不足的情况下,一些航空公司会推出特价机票。一趟A城到B城航班的正常票价是2400元,甲、乙两家航空公司都推出特价票:甲航空公司的机票打二五折,另外要加收20元的手续费;乙航空公司的机票打二八折,免手续费。在哪家航空公司购票更便宜?
参考答案
1.B
【分析】根据左视图和俯视图确定小正方体的最少个数。需要结合两个视图,分析每一列、每一行小正方体的层数,找到最少的情况。
【详解】分析俯视图:俯视图能看到底层小正方体的分布,共有5个小正方形(第一列2个,第二列1个,第三列2个),所以底层至少有5个小正方体。
结合左视图分析层数:左视图有3层,说明几何体在垂直方向上最多有3层。为了让小正方体个数最少,我们要让高层的小正方体尽可能共用底层的。从左视图看,右侧列有3层。对应俯视图的第三列(因为左视图右侧对应几何体的右侧部分),所以第三列的某个小正方体上方可以有2层(因为底层已经算1层,还需2层)。第一列和第二列,根据左视图左侧只有1层,所以这两列最多1层(底层已经满足,不需要额外增加层数)。计算最少个数:底层5个,然后在第三列的一个小正方体上再叠2个(这样高层只需要2个,就能满足左视图的3层),所以总数是5+2=7(个)。
故答案为:B
2.B
【分析】已知x∶y=4∶5,把x看作4份,y看作5份,先用减法求出x比y少的份数,再除以y的份数,即可求出x比y少百分之几。
【详解】(5-4)÷5×100%
=1÷5×100%
=0.2×100%
=20%
已知x∶y=4∶5,那么x比y少20%。
故答案为:B
3.D
【分析】单式折线统计图用于展示一组数据的变化趋势;复式折线统计图用于对比两组相关数据的变化趋势;扇形统计图用于展示各部分在总体中所占的比例关系;条形统计图用于直观比较不同类别数据的数量多少;最后根据各选项的数据特点依次判断即可解得。
【详解】A.某品牌电动车2020-2024年销售情况只涉及到一个品牌电动车不同年份销量,适用单式折线统计图;
B.小力家各项支出占总支出百分比情况重点关注各部分占比情况,适用扇形统计图;
C.六年级各班人数情况比较各班人数,适用条形统计图;
D.北京和上海全年各月平均气温变化情况重点关注两组数据变化趋势,适用复式折线统计图。
故答案为:D
4.B
【分析】根据不同的优惠规则计算出具体的金额:
甲商店打“八五折”销售即将原价乘85%计算出售价,总花费等于打折后售价乘50,代入数据即可;
乙商店“买四赠一”相当于买5本只需要付4本的钱,计算50本里含有“4送1”的组数,总花等于组数乘每组花费,代入数据即可;
丙商店“每满100元减20元现金”,可以先计算出单价乘50,再看能减多少次20元,代入数据即可;
最后将三家的花费进行比较即可。
甲商场花费382.5元,乙商场花费360元,丙商场花费370元。
360<370<382.5所以乙商场花费最少,最划算。
故答案为:B
5.D
【分析】如图所示,小圆的直径等于大圆的半径,设小圆半径是1,则大圆半径是2,根据C=2πr,S=πr2计算周长和面积,再依据求A是B的几分之几用A÷B解答。
【详解】设小圆半径是1,则大圆半径是2
2π×1÷(2π×2)
=2π÷4π
=
π×12÷(π×22)
=π÷4π
=
所以小圆周长是大圆周长的,小圆面积是大圆面积的。
故答案为:D
6.A
【分析】两条圆形轨道相差的长度就是它们周长之差。若1号轨道的半径是 r,2号轨道的半径便是 r+3米,根据圆的周长=2×圆周率×半径,两条圆的周长差=2π(r+3)-2πr;据此计算解答。
【详解】2π(r+3)-2πr
=2π×[(r+3)-r]
=2π×[r+3-r]
=2π×3
=6π(米)
6π≈6×3.14=18.84(米)
不到20米,淘气说的对。
故答案为:A
7.10;16;80;0.8
【分析】根据分数的基本性质来求解第一个括号里的数。分数的基本性质是:分数的分子和分母同时乘或者除以相同的数(0除外),分数的大小不变。
根据分数与比之间的关系来写第二个括号里的数。分数的分子相当于比的前项,分母相当于比的后项。
用分数的分子除以分母得到小数,然后把小数转化成百分数,以此填写后两个空。
【详解】分子从4变成8,是乘了2。根据分数的基本性质,分母也要乘2,5×2=10,所以括号里填10。即;
分母5变成后项20,是乘了4。根据分数与比的关系,分子也要乘4,4×4=16,所以括号里填16。即=16∶20;
4÷5=0.8=80%
8.4.8
【分析】已知一套彩笔定价36元,售出后可获利50%,即定价比进价高50%,把彩笔的进价看作单位“1”,定价是进价的(1+50%),单位“1”未知,用定价除以(1+50%),求出进价;
如果按定价的八折出售,即按定价的80%出售,根据求一个数的百分之几是多少,用定价乘80%,求出售价;再用售价减去进价,就是获利。
【详解】进价:
36÷(1+50%)
=36÷(1+0.5)
=36÷1.5
=24(元)
按定价的八折出售的售价:
36×80%
=36×0.8
=28.8(元)
获利:28.8-24=4.8(元)
如果按定价的八折出售,可获利4.8元。
9. 64 256
【分析】已知圆形窗花的面积是200.96平方厘米,根据圆的面积公式S=πr2,可知半径的平方r2=S÷π,进而得出圆的半径。
用来裁剪该窗花的最小正方形的边长等于圆的直径,根据圆的直径=半径×2,求出正方形的边长;
再根据正方形的周长=边长×4,正方形的面积=边长×边长,分别求出最小正方形的周长和面积。
【详解】半径的平方:200.96÷3.14=64(平方厘米)
因为64=8×8,所以圆的半径是8厘米;
圆的直径(正方形的边长):8×2=16(厘米)
正方形的周长:16×4=64(厘米)
正方形的面积:16×16=256(平方厘米)
所以,用来裁剪该窗花的最小正方形的周长是(64)厘米,面积是(256)平方厘米。
10.(1)已复制的文件占总文件的68%
(2)200
【分析】(1)百分数表示一个数是另一个数的百分之几。图中68%表示的意义是:已复制的文件大小占这份文件总大小的68%。
(2)已复制136M,且已复制的部分占总文件的68%。将总文件的大小看作单位“1”,根据“已知一个数的百分之几是多少,求这个数用除法”,可得这份文件的总大小为136÷68%=200M。
【详解】(1)68%表示的意义是:已复制的文件大小占这份文件总大小的68%。
(2)136÷68%
=136÷0.68
=200(M)
这份文件一共有200M。
11.见详解
【分析】第一幅图房子在左,树在右,是在位置B看到的;
第二幅图正对着树,房子在树的后面,是在位置C看到的;
第三幅图房子在右,树在左,是在位置D看到的;
第四幅图看到的是房子的侧面,树被房子挡住了一部分,是在位置A看到的,据此解答。
【详解】如图:
12. 18.84 3 28.26cm2/28.26平方厘米
【分析】如图所示,剪开后得到的三角形的底等于圆形的周长,高是圆形的半径,根据C=2πr,S三角形=ah÷2计算解答。
【详解】2×3.14×3
=6.28×3
=18.84(cm)
18.84×3÷2
=56.52÷2
=28.26(cm2)
故得到的三角形底是18.84cm,高是3cm,面积是28.26cm2。
13.
×
【分析】根据圆的周长公式,周长与直径的比值是圆周率π,而π的近似值为3.14,但并非精确等于3.14。
【详解】圆的周长公式为:周长=π×直径,其中π是一个固定不变的数,约等于3.1416。题目中“3.14”是π的近似值,并非准确倍数。因此,圆的周长总是直径的π倍,而非精确的3.14倍,原题说法错误。
故答案为:×
14.
√
【分析】根据题意,甲分到的苹果比乙多,这里的是以乙的数量为基准。根据分数的意义,可以把乙分到的苹果看作5份,甲分到的比乙多1份,即6份,因此甲、乙的苹果数量比为6∶5。
【详解】通过分析可得:根据分数的意义,把乙分到的苹果看作5份,5+1=6,则甲、乙分到的苹果个数比为6∶5,原题说法正确。
故答案为:√
15.
×
【分析】采用单循环赛,即每两名同学都要赛一场。现有10名学生参加,第1名学生需要和其余9名学生比赛,即赛9场;第2名学生需要和其余8名学生比赛(已经和第1名学生比过),即赛8场;第3名学生需要和其余7名学生比赛(已经和前两名学生比过),即赛7场……以此类推,总共需要比赛9+8+7+…+3+2+1=45场,据此判断。
【详解】9+8+7+6+5+4+3+2+1
=5×9
=45(场)
所以需要比赛45场,而非20场。
故答案为:×
16.×
【分析】分析题目,可以假设这种商品的原价是100元,先把原价看作单位“1”,用原价乘(1+15%)即可求出涨价之后的价格;再把涨价后的价格看作单位“1”,用涨价后的价格乘(1-15%)即可求出降价后的价格,最后把原价和现价进行比较即可判断。
【详解】假设这种商品的原价是100元。
100×(1+15%)×(1-15%)
=100×115%×85%
=115×0.85
=97.75(元)
100>97.75
一种商品先涨价15%,再降价15%。它的价格发生了改变。
故答案为:×
17.×
【分析】条形统计图可以直观地看出数量的多少;折线统计图不仅能看清数量的多少,还能反映数量的增减变化情况;扇形统计图能清楚地看出各部分数量与总数量之间的关系,据此分析。
【详解】通过分析可得:要表示小林在一天中进行各种活动所用的时间是多少,用条形统计图最合适,所以原题说法错误。
故答案为:×
18.700;1;10
;;2
【详解】略
19.;3;
【分析】,先算乘法,再算除法。
36×(),利用乘法分配律进行计算。
25×,把百分数转化为分数,根据分数的除法运算法则,把除法转化为乘法,然后利用乘法分配律逆运算进行计算。
20.x=80;;x=3
【分析】根据等式的性质1,方程的两边同时加上25%x,交换等号两边的位置将方程化为:100+25%x=120。将方程两边同时减去100,再同时除以0.25即可。
先计算方程左边,将方程化为:x=6,再根据等式的性质2,方程的两边同时除以即可。
根据等式的性质1,方程的两边同时加上1,再根据等式的性质2,方程的两边同时除以即可。
【详解】120-25%x=100
解:120-25%x+25%x=100+25%x
120=100+25%x
100+25%x=120
100+25%x-100=120-100
25%x=20
25%x÷0.25=20÷0.25
x=80
解:x=6
x÷=6÷
x=6×
x=
解:x-1+1=+1
x=
x÷=÷
x=×
x=3
21.17.72平方厘米
【分析】看图可知,阴影部分的面积=梯形面积-半圆的面积,梯形面积=(上底+下底)×高÷2,半圆的面积=圆周率×半径的平方÷2,据此列式计算。
【详解】(5+7)×4÷2-3.14×(4÷2)2÷2
=12×4÷2-3.14×22÷2
=24-3.14×4÷2
=24-6.28
=17.72(平方厘米)
阴影部分的面积是17.72平方厘米。
22.见详解
【分析】观察立体图形,从前面能看到两层4个小正方形,下层有3个,上层有1个且居左;从左面能看到两层3个小正方形,下层有2个,上层有1个且居左;从上面能看到三列4个小正方形,左列1个且居上,中列2个,右列1个且居下;据此画出从前面、左面、上面看到的形状。
【详解】如图:
23.见详解
【分析】甲村有耕地250公顷;根据统计图可知,花生种植面积是25公顷,用花生种植面积÷甲村耕地面积×100%,求出花生种植面积占耕地面积的百分比。把甲村耕地面积看作单位“1”,用1减去花生占耕地面积的百分比,减去甘蔗占耕地面积的百分比,减去棉花占耕地面积的百分比,求出水稻占耕地面积的百分比;完成扇形统计图。
用甲村的耕地面积×甘蔗占耕地面积的百分比,求出甘蔗种植面积;用甲村耕地面积×棉花占耕地面积的百分比,求出棉花种植面积;再用甲村的耕地面积×水稻占耕地面积的百分比,求出水稻种植面积;完成条形统计图。
【详解】花生:
25÷250×100%
=0.1×100%
=10%
水稻:
1-10%-18%-26%
=90%-18%-26%
=72%-26%
=46%
如下图:
甘蔗:250×18%=45(公顷)
棉花:250×26%=65(公顷)
水稻:250×46%=115(公顷)
如下图:
24.250千克
【分析】原计划每个零件需用钢材千克,改进技术后每个零件所用钢材比原来节约,把原计划每个零件需用钢材看作单位“1”,那么改进后每个零件所需钢材是原来的(1-)。所以改进后每个零件所需钢材重量为:×(1-)千克。已知改进后每个零件需钢材×(1-)千克,那么做400个零件需要的钢材重量,就是用×(1-)乘400计算即可。
【详解】把原计划每个零件需用钢材看作单位“1”。
×(1-)×400
=××400
=×400
=250(千克)
答:现在做400个这样的零件需要钢材250千克。
25.150平方厘米
【分析】三条边长度比为3∶4∶5,总份数为3+4+5=12份。已知周长是60厘米,所以每份长度为60÷12=5厘米。对应“3份”的边:5×3=15厘米,对应“4份”的边:5×4=20厘米,对应“5份”的边:5×5=25厘米。直角三角形中,最长边(25厘米)是斜边,两条较短边(15厘米、20厘米)是直角边(互为底和高)。根据面积公式:面积=底×高÷2,把数据代入计算即可。
【详解】3+4+5=12(份)
60÷12=5(厘米)
5×3=15(厘米)
5×4=20(厘米)
5×5=25(厘米)
20×15÷2=150(平方厘米)
答:它的面积是150平方厘米。
26.A卷
【分析】先算出A卷剩下的长度占总长的几分之几,将总长看作单位“1”,再用分数乘法得出A卷剩下的长度;将B卷的总长看作单位“1”,用B卷的总长乘剩下的百分数得出B卷剩下的长度,最后作比较即可。
【详解】A卷:
B卷:
7米<8米<9米
答:李老师应该选择A卷彩纸比较合适。
27.71.4米;121.5平方米
【分析】观察可知,广场的周长等于两个圆周长的一半(即一个圆的周长)加上长方形的两条长,根据圆的周长公式,代入数据计算即可得广场的周长;草坪的面积等于长方形的面积减两个半圆的面积(即一个圆的面积),根据圆的面积公式,代入数据计算即可。
【详解】3.14×10+20×2
=31.4+40
=71.4(米)
(平方米)
答:广场的周长是71.4米;草坪的面积是121.5平方米。
28.
甲航空公司
【分析】已知正常票价是2400元,甲航空公司的机票打二五折,另外要加收20元的手续费。打二五折就是按原价的25%收费,所以甲航空公司的机票费用为2400×25%+20。
已知乙航空公司的机票打二八折,免手续费。打二八折就是按原价的28%收费,所以乙航空公司的机票费用为2400×28%。
分别计算出甲、乙两家航空公司的票价,进行比较即可。
【详解】2400×25%+20
=2400×0.25+20
=600+20
=620(元)
2400×28%
=2400×0.28
=672(元)
620<672
答:在甲航空公司购票更便宜。
